作为FDS的收尾, 补充几个主要是和图有关的算法
前言
大纲
带负权边最短路径 | Bellman-ford算法与SPFA算法
双连通性 | Tarjan算法
AOE网络与网络流
哈希算法
参考资料
正文-上
在求解有关最小路径问题 的时候, 我们常用的算法是Dijsktra算法和Floyd算法, 这两种算法虽好, 但是对于带负权边图却无能为力. 对于带负权边图的最小路径问题, 我们一般采用Bellman-ford算法及其优化版本SPFA算法.
Bellman-ford算法
与Dijsktra算法的不同
与采用贪心算法进行松弛操作的Dijsktra算法不同, Bellman-ford算法直接对所有边进行松弛, 这在导致其时间复杂度增加至O ( ∣ V ∣ ∣ E ∣ ) O(|V||E|) O ( ∣ V ∣∣ E ∣ )
伪代码描述
相比于使用了贪心算法的Dijsktra算法, Bellman-ford算法的实现思路更加大开大合, 因此代码书写也更为简单.
下面伪代码描述了一个有n个节点和m条边的图的算法模板, 图的储存方法是储存每一条边
//求解节点0~k的最短路径, 如果存在负环或不连通, 则返回-1 int bellman-ford( vertex k ){ dis[n]={INF}; dis[s]=0; //初始化源点S到各个点V的距离为INF, 到自己的距离为0 for i:0->(n-1){ //(n-1)次遍历 for j:0->m{ //对所有边进行松弛 e = edge[j]; if(dis[e.start] + e.weight < dis[e.end]){ dis[e.end] = dis[e.start] + e.weight; //如果经过e能使s到e.end更近, 就更新之 } } } //负环图判断 //如果能得到更近路线, 说明存在负环 for j:0->m{ if(dis[e.start] + e.weight < dis[e.end]){ return -1; } } //负环图判断结束 if(dis[k]==INF){ return -1; } return dis[k]; }
SPFA算法优化
通过上面的分析, 我们可以归纳Bellman-ford算法的底层逻辑: 暴力遍历, 无脑松弛 . 这样的逻辑很有效, 但是如果我们可以通过剪枝降低所花费的时间, 那他会更美.
SPFA算法能降低实际花费的时间(然而时间复杂度仍为O ( ∣ V ∣ ∣ E ∣ ) O(|V||E|) O ( ∣ V ∣∣ E ∣ )
我们通过构造一个队列q, 维护要进行松弛操作的节点, 我们可以用伪代码进行描述(注意这个图是由邻接表map储存的)
//求解节点0~k的最短路径, 如果存在负环或不连通, 则返回-1 int spfa( vertex k ){ dis[n]={INF}; dis[s]=0; //初始化源点S到各个点V的距离为INF, 到自己的距离为0 visited[n]={0}; //初始化所有节点均未访问 queue q; //初始化维护队列 q.push(s); visited[s]=1; //源点入队 while( !q.empty() ){ t = q.pop(); visited[t] = 0; //队首出队,开始遍历 for i:0->map[t].size(){ e = map[t][i]; if( dis[t] + e.weight < dis[e.end] ){ //选取所有以t为起点边进行松弛操作 dis[e.end] = dis[t] + e.weight; if( visited[e.end] == 0 ){ //如果被松弛的节点未入队, 则入队 q.push(e.end); visited[e.end] = 1; } } } } if(dis[k]==INF){ return -1; } return dis[k]; }
当然, 除了队列以外, 栈, 堆都可以用来进行优化.
例题
正文-下
参考资料
CSDN | Tarjan算法超超超详解(ACM/OI)(强连通分量/缩点)(图论)(C++)
一些概念
割点 : 如果去掉一个点,剩下的图不再是连通的,则称这个点为割点双连通性 : 如果一个无向连通图没有割点, 则我们称之为双连通图强连通性 : 如果一个有向连通图没有割点, 则我们称之为强连通图双连通分量 : 极大的双连通子图强连通分量 : 极大的强连通子图
从DFS开始
考虑一个DFS遍历图的算法, 为方便和理解起见, 我们采用邻接矩阵 储存这个图.
#include <iostream> using namespace std;class Graph {public : Graph (int _N, int _M); void DFS (int S) private : int N, M; int matrix[55 ][55 ] = {0 }; void dfs (int V, bool visited[]) }; Graph::Graph (int _N, int _M){ N=_N; M=_M; for (int i=0 ;i<M;++i){ int start, end; cin>>start>>end; matrix[start][end] = 1 ; } } void Graph::DFS (int S) bool visited[55 ] = {0 }; dfs (S, visited); cout<<endl; } void Graph::dfs (int V, bool visited[]) visited[V] = true ; cout<<V<<'#' ; for (int W=1 ;W<=N;++W){ if (matrix[V][W] == 1 && visited[W] == 0 ){ dfs (W,visited); } } } int main () Graph graph (7 ,9 ) ; graph.DFS (1 ); }
时间戳
为了更方便的查找每一个节点的访问顺序, 我们可以引入时间戳 的概念对DFS函数进行修改, 这样, 越早被访问的节点有着越小的时间戳dfn[V], 且不存在任意两个节点有着一样的时间戳
class Graph {public : Graph (int _N, int _M); void DFS (int S) private : int N, M; int matrix[55 ][55 ] = {0 }; void dfs (int V, bool visited[], int & cur) int dfn[55 ] = {0 }; }; void Graph::DFS (int S) bool visited[55 ] = {0 }; int cur = 0 ; dfs (S, visited, cur); cout<<endl; } void Graph::dfs (int V, bool visited[], int & cur) ++cur; dfn[V] = cur; visited[V] = true ; cout<<V<<'#' ; for (int W=1 ;W<=N;++W){ if (matrix[V][W] == 1 && visited[W] == 0 ){ dfs (W,visited, cur); } } }
边的分类
根据DFS过程, 我们可以将边做以下分类
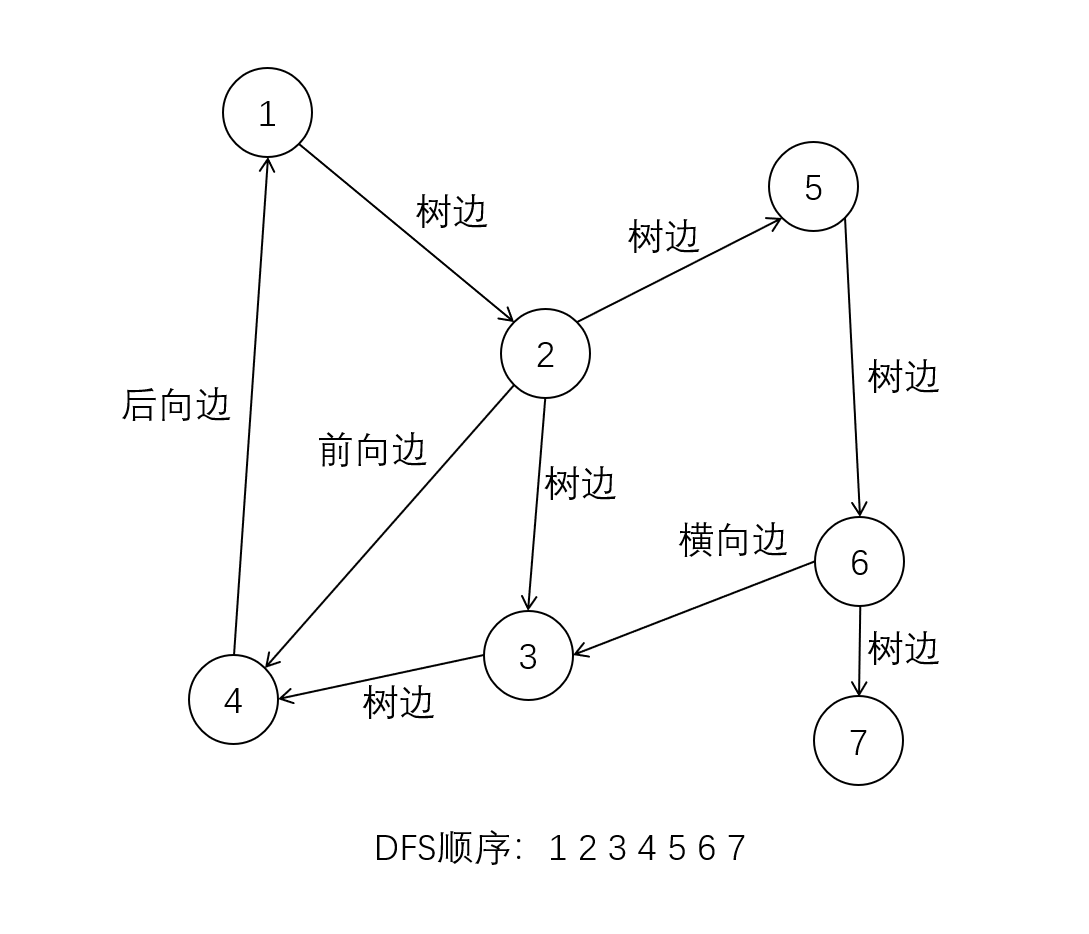
树边 : DFS搜索树上的边, 用代码解释就是条件判断matrix[V][W] == 1 && visited[W] == 0为true的边后向边 : DFS搜索树上, 子孙节点V指向祖先节点W的边, 虽然我们不能通过代码判断后向边, 但是我们可以证明后向边<V,W>一定满足matrix[V][W]==true && dfn[V] > dfn[W]前向边 : 与后向边相对, 指DFS搜索树上, 祖先节点W指向子孙节点V的边, 我们同样不能靠代码判断, 但是对于前向边<W,V>我们也有以下条件表达式matrix[W][V]==true && dfn[V] > dfn[W]横向边 : 除去上述三种边以外的边, 我们统称为横向边
关于这几种边, 我们将代码中的测试数据画成图理解一下
关于横向边, 我们有如下性质(证明请移步 )
横向边<V,W>满足dfn[V]>dfn[W]
若有横向边<V,W>, 则不存在路径V->W
强连通分量
我们判断强连通分量的任务就是判断后向边的任务.
注意到后向边和横向边<V,W>均满足dfn[V]>dfn[W], 所以我们不能依靠这个判断, 我们可以考虑维护一个搜索栈 st–对于后向边<V,W>, 访问V时, 我们可以发现W已经在搜索栈内, 因此<V,W>是后向边; 对于横向边则没有上述性质.
我们可以借由数组instack[]完成操作
void Graph::DFS (int S) bool visited[55 ] = {0 }; int cur = 0 ; stack<int > st; bool instack[55 ] = {false }; dfs (S, visited, cur, st, instack); cout<<endl; } void Graph::dfs (int V, bool visited[], int & cur, stack<int >& st, bool instack[]) ++cur; dfn[V] = cur; st.push (V); instack[V] = true ; visited[V] = true ; cout<<V<<'#' ; for (int W=1 ;W<=N;++W){ if (matrix[V][W] == 1 && visited[W] == 0 ){ dfs (W,visited, cur, st, instack); } else if ( matrix[V][W] == 1 && instack[W] == true ){ ; } } st.pop (); instack[V] = false ; }
Tarjan算法
知道了后向边<V,W>之后, 我们可以做什么呐?
当然是求强连通分量了!
根据我们上一小节提出的定理, 我们需要一个方法标注路径V->W上所有的元素都属一个强连通分量. 对此我们可以引入追溯值数组low[], 其中low[V]表示含有V的强连通分量第一个被访问的节点的时间戳dfn[V'].
对于后向边<V,W>, 显然路径W->V上任何一个节点T的追溯值low[T]都应该等于dfn[W](也就是low[W], 这里推荐前者)
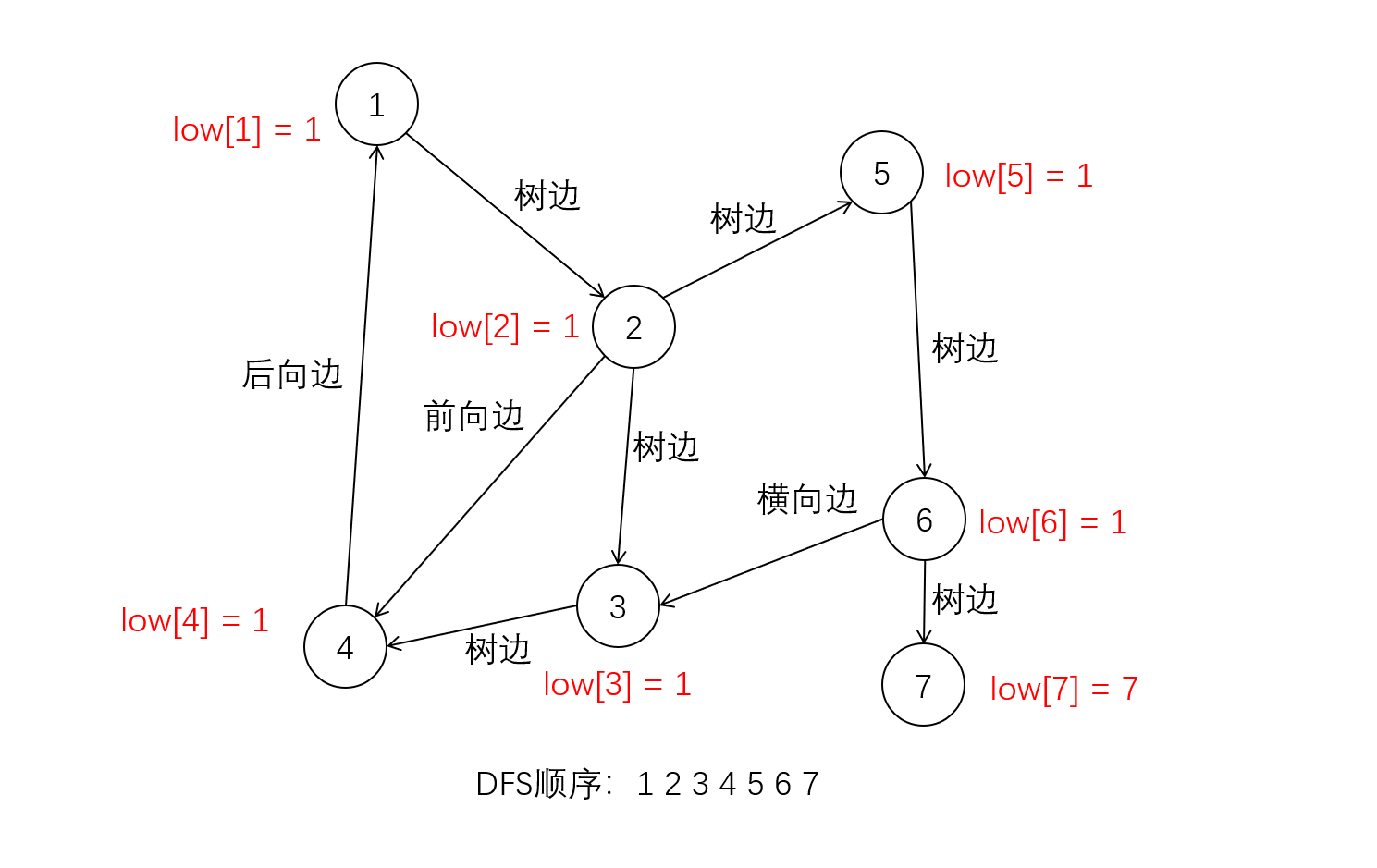
对于我们给出的测试数据, 更新追溯值之后的图应该是这样的
解释: 由于存在后向边<4,1>, 路径1->2->3->4和1->2->5->6->3->4->1上所有节点的追溯值low[i]均为dfn[1], 而节点7不存在强连通分量, 则他们的追溯值low[i]等于dfn[i]
理解了追溯值的概念, 那我们要考虑如何更新追溯值了. 一种方法是我们在发现后向边的时候对搜索栈中符合条件的节点都更新一次追溯值, 这种方法有一定的可行度, 但是既不简洁, 也不美丽. 我们可以在回溯的时候进行一次判断: 假如当前节点的追溯值大于了子节点的追溯值, 则更新为子节点的追溯值
代码实现如下
void Graph::dfs (int V, bool visited[], int & cur, stack<int >& st, bool instack[]) ++cur; dfn[V] = cur; low[V] = cur; st.push (V); instack[V] = true ; visited[V] = true ; cout<<V<<'#' ; for (int W=1 ;W<=N;++W){ if (matrix[V][W] == 1 && visited[W] == 0 ){ dfs (W,visited, cur, st, instack); low[V] = min (low[V], low[W]); } else if ( matrix[V][W] == 1 && instack[W] == true ){ low[V] = min (low[V], dfn[W]); } } st.pop (); instack[V] = false ; }
最后我们考虑标记每一个强连通分量, 我们定义标记数组sign[], 假如节点V属于第i个强连通分量, 则sign[V] = i.
做标记的时间点不应该与更新追溯值同时, 我们可以在回溯到强连通分量最先被访问的节点时, 对搜索栈st进行一个出栈标记的操作.
完成以上所有操作后, 我们就可以将DFS函数改写为Tarjan函数了, 代码实现如下(感恩@Watertomato 帮忙debug!!!)
#include <iostream> #include <stack> using namespace std;class Graph {public : Graph (int _N, int _M); void Tarjan (int S) private : int N, M; int matrix[55 ][55 ] = {0 }; void dfs (int V, int & cur, stack<int >& st, bool instack[]) int dfn[55 ] = {0 }; int low[55 ] = {0 }; int sign[55 ] = {0 }; int cnt = 0 ; int min (int x, int y) return x>y? y:x; }; }; Graph::Graph (int _N, int _M){ N=_N; M=_M; for (int i=0 ;i<M;++i){ int start, end; cin>>start>>end; matrix[start][end] = 1 ; } } void Graph::Tarjan (int S) int cur = 0 ; stack<int > st; bool instack[55 ] = {false }; dfs (S, cur, st, instack); cout<<endl; } void Graph::dfs (int V, int & cur, stack<int >& st, bool instack[]) ++cur; dfn[V] = cur; low[V] = cur; st.push (V); instack[V] = true ; cout<<V<<'#' ; for (int W=1 ;W<=N;++W){ if (matrix[V][W] == 1 && dfn[W] == 0 ){ dfs (W, cur, st, instack); low[V] = min (low[V], low[W]); } else if ( matrix[V][W] == 1 && instack[W] == true ){ low[V] = min (low[V], low[W]); } } if (low[V] == dfn[V]){ ++cnt; do { int tmp = st.top (); st.pop (); sign[ tmp ] = cnt; instack[ tmp ] = false ; cout<<tmp<<" in " <<cnt<<endl; if ( tmp == V ) break ; }while (true ); } } int main () Graph graph (7 ,9 ) ; graph.Tarjan (1 ); }
后记
略, 太累了写完这个Tarjan算法, 主要是一直被一个蠢蠢的bug卡着>-<