可能大概是最后一篇自学FDS的笔记了, 解决最后两个问题
残月: 古人对十二月的雅称, 在此表示最后几篇文章

前言

大纲

  • AOE网络与网络流
  • 哈希算法

 

参考资料

 

正文-上

AOE网络

AOE(activity on edge)网络是一张有向带权图, 其中有向边代表活动, 权值代表活动持续的时间.

 

关键路径

一个AOE网络有且仅有一个入度为0的节点, 我们称之为源点S; 以及一个出度为0的节点, 我们称之为汇点T. 我们将源点的时间戳记作0.

节点是一个时间概念, 表示两项活动之间的间隔, 这个间隔有长有短. 对于任意一个节点(S,T除外), 当且仅当进入节点的活动全部完成, 离开节点的活动才能开始.

为了保证工期的按时完成, 我们要保证那些绝对不能拖延的活动按时完成, 由这些活动构成的路径, 我们称为关键路径.

 

节点的时间

对于任何一个节点, 我们存在一个最早发生时间EHT[]和最晚发生时间LHT[].

  • 最早发生时间: 指对于节点V来说, 所有他的前提节点U都完成的时间点. 因为只有所有前提节点U都完成时, 节点V才能发生, 递推公式可写作
    • EHT[V] = 0(当V为源点S)
    • EHT[V] = max{ EHT[U] + <U,V> }(当V不是源点S, 其中U为任意前提节点)
  • 最晚发生时间: 指对于节点V来说, 能不使后继节点W的最晚发生时间延长的最晚时间. 听着可能有点绕, 举个例子, W有前提节点V1和V2, 假设V1和V2有相同的最早发生时间, <V1,W>=30, <V2,W>=100, 那么, 只要我们在V1节点磨蹭的时间x<=70, W都可以在t=100的时候发生, 这时我们说V1的最晚发生时间是70. 递推公式可写作
    • LHT[V] = LHT[V](当V为汇点T, 我们认为其最早发生时间就是工期)
    • LHT[V] = min{ LHT[W] - <V,W> }(当V不是汇点T, 其中W为任意后继节点)

 

边的时间

知道了任意节点的最早发生时间和最晚发生时间, 我们可以对边的时间要求做出更详细的描述.

对于<V,W>, 存在松弛时间ST = LHT[W] - EHT[V] -<V,W> . 松弛时间表示能在该边延误的最长时间. 假如存在松弛时间为0的边构成的一条路径, 则该路径是关键路径.

 

AOV网络

AOV(activity on vertex)网络与AOE网络相对, 是将节点作为活动. 对于求解有关AOV网络的问题, 我们一般使用拓扑排序.

拓扑序: 如果在AOV网络中, 存在路径V->W, 则相应的排序中V也在W前面, 则这样的排序结果我们称为拓扑序.

  • 一个AOV网络的拓扑序不一定是唯一的.
  • 一个AOV网络如果有拓扑序, 则一定是一个DAG(有向无环图).

 

拓扑排序

拓扑排序的思路就是, 每次取出入度为0的节点(因为入度为0的节点没有了前驱, 一定是能发生的)入队, 并在出队时调整该节点后驱的入度. 伪代码描述如下

auto toposort(Graph G){
    Queue q;
    Vector v;   //储存排序后的结果, 也可以直接输出拓扑序
    int cnt = 0;
    for V:0->N{ //初始将所有入度为0的节点入队
        if( V.indegree == 0 ){
            q.push(V);
        }
    }
    while(q){
        V = q.pop();
        v.push(V);
        ++cnt;
        //对所有V的后驱W进行操作
        for W:0->N{
            if( <V,W> == 1 ){
                --W.indegree;
                //如果减去这个入度后, W的入度为0, 则入队
                if( W.indegree == 0 ){
                    q.push(W);
                }
            }
        }
    }
    if( cnt != N ){ //如果只排序了不到N个节点, 说明存在环导致有的节点的入度无法归零
        return ERROR;
    }
    else{
        return v;
    }
}

 

网络流

类似于水流, 我们可以定义网络图中的流量.

对于给定有向图G, 定义唯一的源点S和唯一的汇点T, S和T的定义均和AOV,AOE的定义相似, 不同的是, 网络流中每条边<U,V>均有一个最大容量c(U,V). 我们将上述网络流记作G(V,E,c).

 

可行流

对于G(V,E,C), 若给每条边<U,V>给定一个流量f(U,V), 使0<=f(U,V)<=c(U,V)对于任意一条边均为true, 且满足以下条件:

  • S的流出量 = 网络的流量和 = T的汇入量
  • 对任意节点均有: 汇入量之和 = 流出量之和

对于满足以上条件的f(U,V)的集合, 我们称之为可行流.

注意: f(U,V)既不能大于c(U,V), 也不能小于0(即出现负流量的情况).

例如, 对于下列网络流

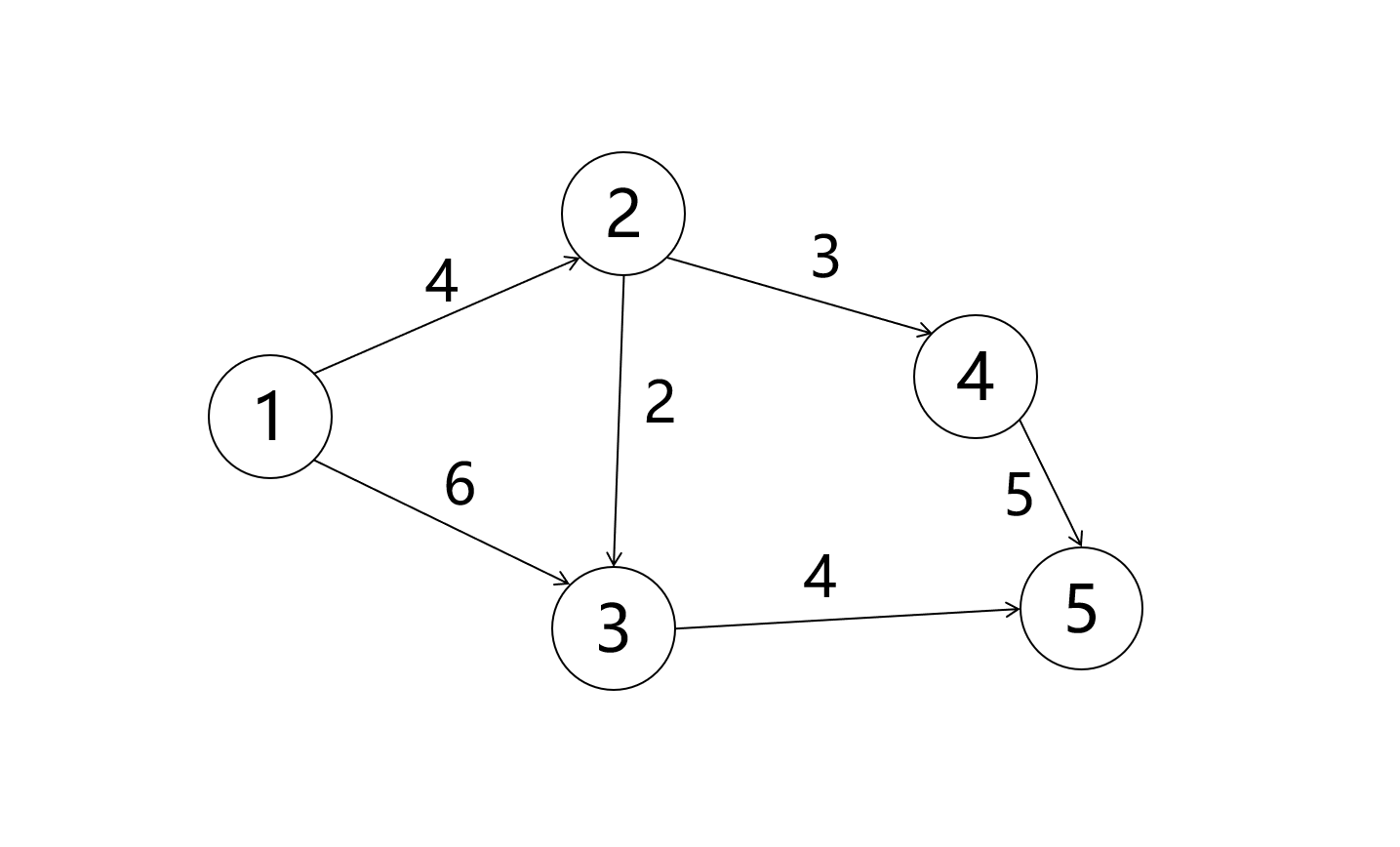
就有多种可行流, 我们选取其中两种

 

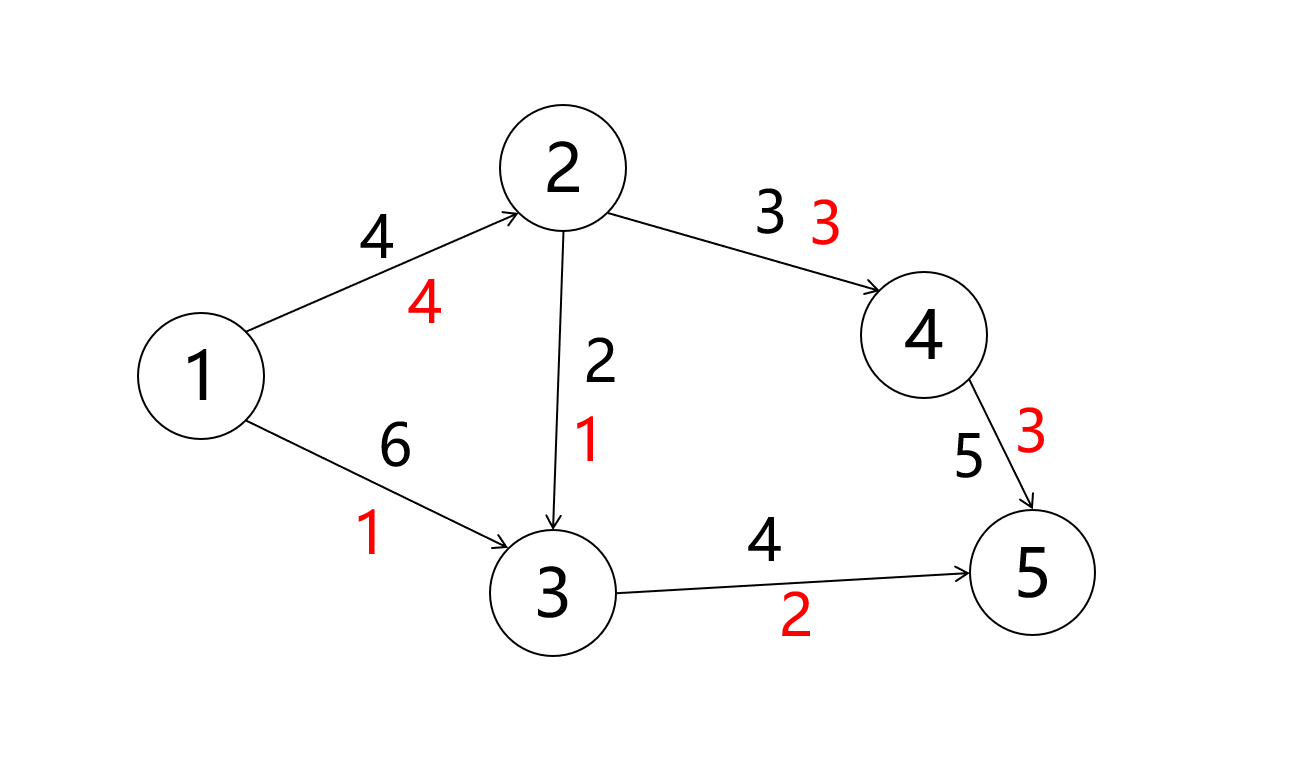
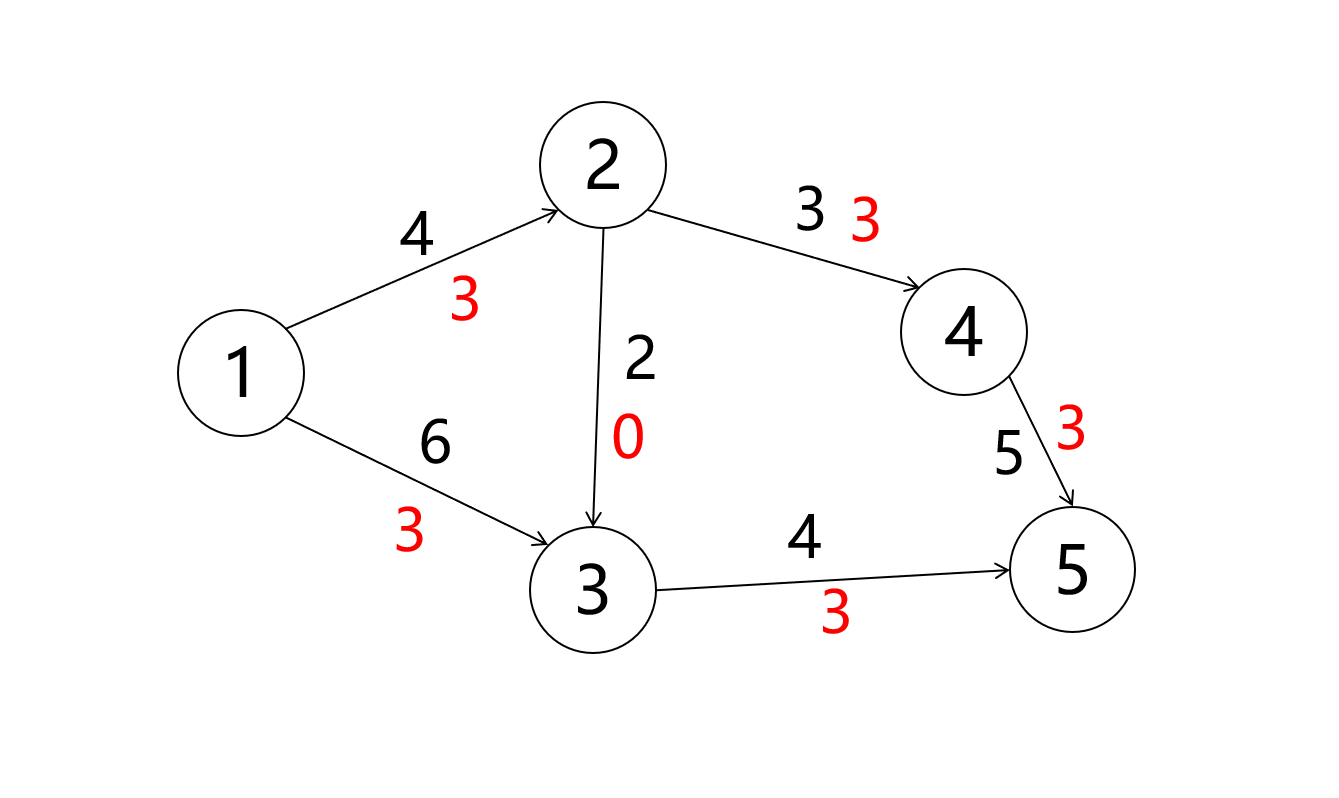
最大流

在所有可行流中, 我们关注流量最大流–最大流.

在最大流问题中, 流量f和容量c满足以下条件:

  • f(U,V)≤c(U,V)f(U,V)\le c(U,V)
  • f(U,V)=−f(V,U)f(U,V) = -f(V,U)
  • ∑<U,V>∈Ef(U,V)=0,(U≠S,U≠T)\displaystyle\sum_{<U,V>\in E}f(U,V) = 0,(U\ne S,U\ne T)

 

建立残差图

为了求解最大流, 我们需要建立一个残差图, 用来描述每条边的富余容量.

cf(U,V)={c(U,V)−f(U,V),if<U,V>∈Ef(V,U),elif<V,U>∈E0,elsec_f(U,V)=\begin{cases}c(U,V) - f(U,V)&,if<U,V>\in E\\\\ f(V,U)&,elif<V,U>\in E\\\\0&,else\end{cases}

将残差容量,源点S和汇点T组合在一起的新图称为残差图, 记作Gf(V,E,cf)G_f(V,E,c_f)

 

EK增广路算法

洛谷 | P3376 【模板】网络最大流

在残差图Gf(V,E,cf)G_f(V,E,c_f)中, 路径S->T即为增广路.

增广路的流量即是路径上最小残差.

EK算法即是利用增广路不断更新最大流量, 直到不存在增广路为止.

实现思路如下:

  1. 利用BFS寻找并记录一条增广路, 记下增广路的流量(路径上最小边权)
  2. 更新增广路的边权(正向边减去流量, 反向边加上流量)
  3. 重复上述过程, 直到找不到增广路为止

反向边: 在BFS的过程中, 我们无法保证能搜索到所有增广路, 因此我们需要一次反悔的机会. 反向边提供了这样的机会. 当正向边的流量增大时, 反向边的流量减少, 反之亦然. 这样, 当我们两次分别从两个方向经过某一条边, 我们增广的值就能相互抵消, 达到重复遍历的效果.

模板题AC代码如下

#include<iostream>
#include<queue>
#define ll long long
const int MAXN = 205;
const ll MAXLL = 0x7fffffff;
using namespace std;

class Net{
public:
    Net();
    ll EK();
    bool bfs();
    void update(ll& max_flu);
private:
    int n,m,S,T;
    ll net[MAXN][MAXN] = {0};   //初始化网络图
    ll flu[MAXN];               //记录最小的流量
    int pre[MAXN];              //储存回溯路径
};

Net::Net(){
    cin>>n>>m>>S>>T;
    for(int i=0;i<m;++i){
        int u,v,w;
        cin>>u>>v>>w;
        net[u][v] += w;     //这里用+=是因为洛谷的数据有重边
    }
}

ll Net::EK(){
    ll max_flu = 0;
    while( bfs() ){         //一直BFS搜索增广路, 直到不存在增广里
        update(max_flu);    //每条增广路更新一次最大流
    }
    return max_flu;
}

bool Net::bfs(){
    bool visited[MAXN]={false}; //BFS模板
    queue<int> q;
    q.push(S);
    visited[S] = true;
    flu[S] = MAXLL;

    while( !q.empty() ){
        int V = q.front();
        q.pop();

        for(int W=1;W<=n;++W){
            if( net[V][W] == 0 || visited[W] == true ){
                continue;
            }
            else{
                flu[W] = min( flu[V], net[V][W] );  //更新最小流量
                pre[W] = V;
                q.push(W);
                visited[W] = true;
                if( W == T )    return true;
            }        
        }
    }

    return false;
}

void Net::update(ll& max_flu){
    int cur = T;
    do{
        int nxt = pre[cur];
        net[nxt][cur] -= flu[T];    //反向遍减去流量
        net[cur][nxt] += flu[T];    //正向边加上流量
        cur = nxt;
    }while( cur!= S );
    max_flu += flu[T];
}

int main(){
    Net net;    //实例化解决问题的类
    cout<<net.EK()<<endl;   //输出EK算法求解的结果
}

 

后记

哈希的东西比较杂乱, 感觉自学的意义和价值不大, 留个坑吧(逃