Vanadium的小屋

Lecture 2

Splay Tree

Characteristic

1. may not be balanced
2. move a node to root when it is found
3. may not be $O(\log N)$ to each findkey operation but must be $O(\log N)$ after amortized
4. time complexity of $M$ times operation is $O(M\log N)$

Rotation

assume that P is parent, G is grandparent and X is son that is found

1. if P is root, then rotation directly
2. if P is not root, namely G is existing
   1. zig-zag: LR or RL double rotation
   2. zig-zig: 2 times LL or RR single rotation (rotate P firstly, then rotate X)

Findkey

1. find X
2. move X to root

single worst complexity: $O(N)$
amortized single complexity: $O(\log N)$

Insertion

1. find place and insert X
2. move X to root

amortized single complexity: $O(\log N)$

Deletion

1. find X
2. move X to root and delete X, leaving left and right two subtree
3. find the maxinum of left subtree and move it to the root, then apply the right subtree to root

Amortized Analysis

均摊分析指的是一系列操作的代价

worst complexity $\le$ amortized complexity $\le$ average complexity

便于理解, 平均复杂度指的是分布较为阳间的复杂度, 而均摊复杂度是无论分布如何阴间, 都能保持的复杂度, 依赖 adpatbility自适应性

Aggregate Analysis 聚合分析

确定 n 个操作的总代价上界为 $T(n)$，单次平均代价为 $T(n)/n$

Accounting Method 核算法

将操作序列中较早的操作的余额计入 credit, 随后用于支付均摊代价 $\hat c_i$ 和实际代价 $c_i$ 之间的差额

• 银行不能赊账, 即 credit $\ge$ 0
• 可以多个操作一起计算

Potential method 势能法

与核算法类似, 分析每个操作的代价, 但是将势能作为一个整体函数, 与某个对象无关. 操作的摊还代价的计算为操作实际代价加上操作引起的势能变化 (credit)

• define credit function $f(x_n)$, then $\hat{c_i} = c_i + f(x_n) - f(x_{n-1})$
• total amortized operation $\sum\hat{c_i} = \sum(c_i) + f(x_n) - f(x_{n-1})$
  • $\forall 1\le i\le n,f(x_0)<f(x_i)$

Example

Stack Operation

support pop, push and multipop… operations

Binary Counter Operation

Splay Tree Operation

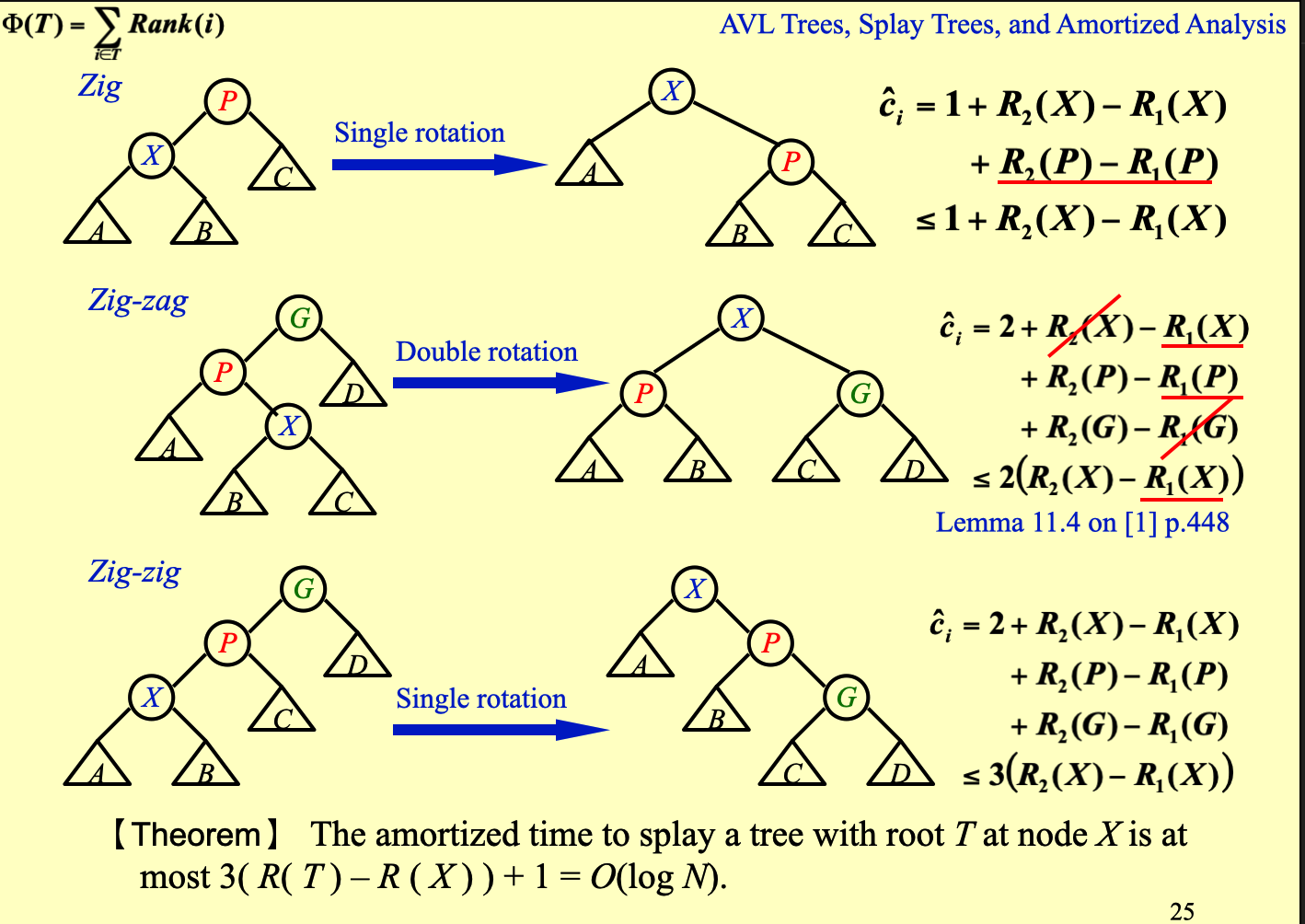
using potential method to analyze
mathematically, we know $a + b \le c\ \text{and}\ a,b,c>0\Rightarrow\log a+\log b\le2\log c-2$

• define $D_i$ is tree
• define potential function $\Phi(T)=\sum \log S(i)$, $S(i)$ means the number of subnodes of node $i$
  • namely the rank of tree
  • approximately equals to the hight of tree, but not changes as frequent as height