计算机系统I(二)

Basic Infomation

Teachers: wht, ll
Lab Docs: 浙江大学24年春夏系统贯通一实验( ZJU intranet required )

Because of some reasons, Chapter 04 should change position with Chapter 05

Chapter 02 Binary Number Representation

Data represantation

Carry Counting System

radix: $r$

digit: $A_{n-1}A_{n-2}...A_1A_0.A_{-1}A_{-2}...A_{-m+1}A_{-m}$

$(100101.01)_2=2^5+2^2+2^0+2^{-2}=(37.25)_1\kern{}_0$

Arithmetic Operators

1. Addition
2. Subtraction
3. Multiplication
4. Division

 

Chapter 03 Representation of Numeric Data

Integer

Focus on binary number with N Bits ( called ${X_T}$ )

$$X_T=X_{n-1}X_{n-2}…X_1X_0$$

Encoding Methods of Integers

Original code

use $X_{n-1}$ as signature

0 owns two representations — +0 & -0

Complement code ( IMPORTANT )

Eg in 12 o’clock

$10 - 4 = 6$

$10 + 8 = 18 \equiv 6 ( \mathrm{mod}\ 12 )$

Definition $\forall X_T: [X_T]_C=M+X_T(\mathrm{mod}\ M)$

The Conversion from Complement code to true value:

• If the sign bit is 0 / the number is positive:
  The value part does not need to be changed
• Else the sign bit is 1 / the number is negative:
  Invert the bits of value part, and add 1 to the result

From $[X_T]_C$ to $[-X_T]_C$:
Invert every bits, and add 1 to to the result

Advantages ( compared with sign-magnitude ):

• No +0 or -0 anymore
• Hardware simplicity

Inverse code

Complexity and uselessness in modern computer

Difference with the complement code Just invert, no add

$-1\rightarrow -0\rightarrow+0\rightarrow 1$

Frameshift code ( more used in float numbers )

TBD

 

Representation of Integers

Bit-Level Operation in C

Bit Operations & | ~ ^ are available in C

Shifting Operations

• Left shift x << y
  Fill with 0 on right
• Right shift x >> y
  Fill with 0 on left ( Logical shift )
  Fill with 0 if positive or 1 if negative ( Arithmetic shift )
• Undefined Behaviour
  Shift amount < 0 or >= word size

 

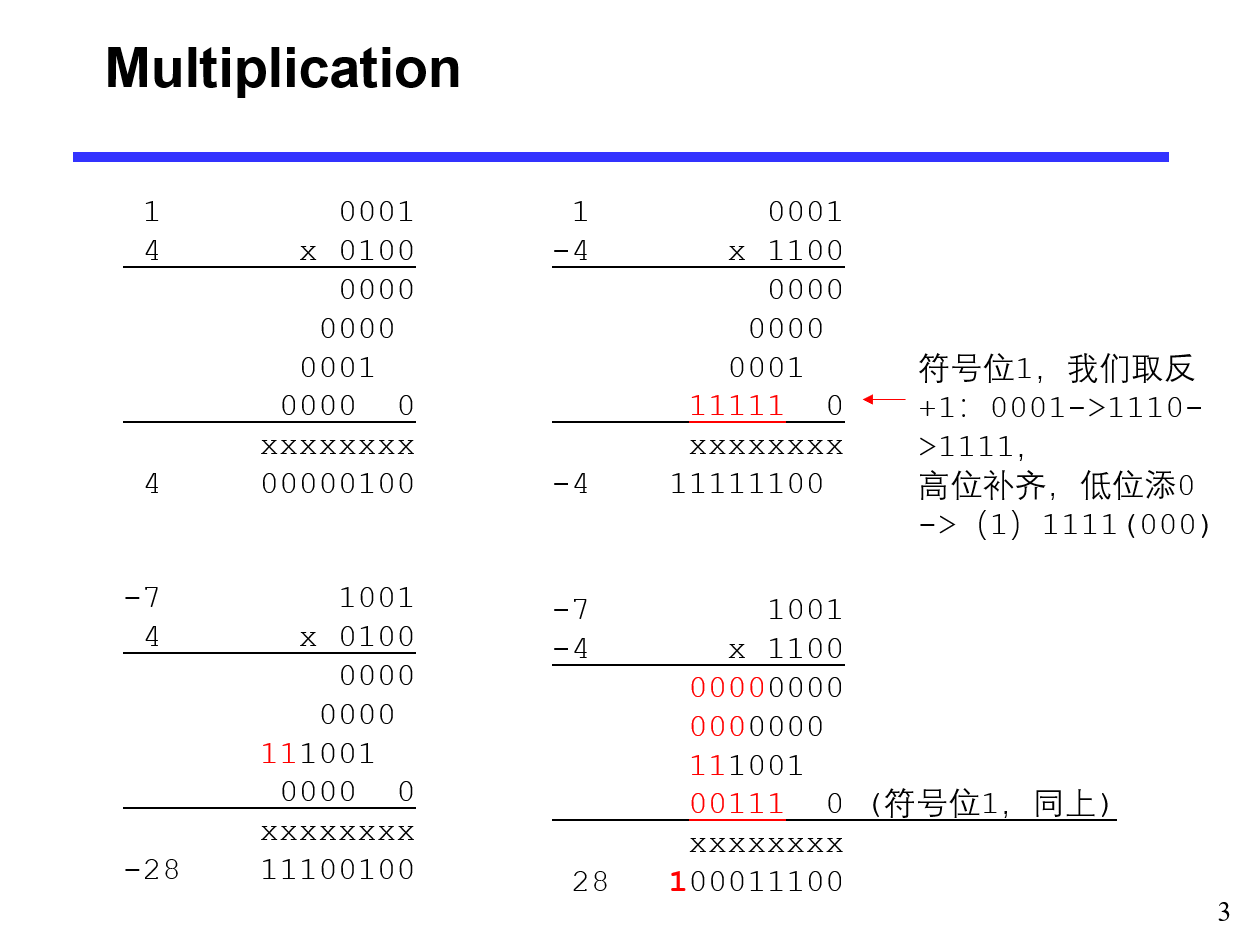
Multiplication

竖式累加的时候用第一位的数字补足每个乘出来的中间数字成一个相同长度的数字，乘数的符号位乘以被乘数时需要取反后加一

 

Chapter 05 Floating-Point Number Representation & Non-Numeric Data

IEEE Standard 754

Numerical Form: $\mathrm{(-1)^sM\cdot2^E}$

• Sign bit s determines positive or negative
• M is in range [1.0, 2.0)
• Exponent E weights value by power 2

 

Precision

• Single precision 32 bits: s=1; exp = 8; frac = 23
• Double precision 64 bits: s = 1; exp = 11; frac = 52
• Extended precison 80 bits (Intel only)

 

Exponent (Frameshift Code)

Before calculation, times each number by $2^{n-2}$ (or frameshift by $(n-2)$ bits), and divide the same number after calculation

the goal is to escape from the case of “deviding zero” and etc.

When turn the component number to the true number, $E=exp-bias$

 

Normalized Encoding

Value: $15213.0_1\kern{}_0=1.1101101101101_2\times2^{13}$

Significand

• M = $1.1101101101101_2$
• frac = $1101101101101000…0_2$

Exponent

• E = $13$
• Bias = $127(=2^{8-1})$
• Exp = $140$ = $10001100_2$

Result

• $0 | 10001100 | 1101101101101000...0$

 

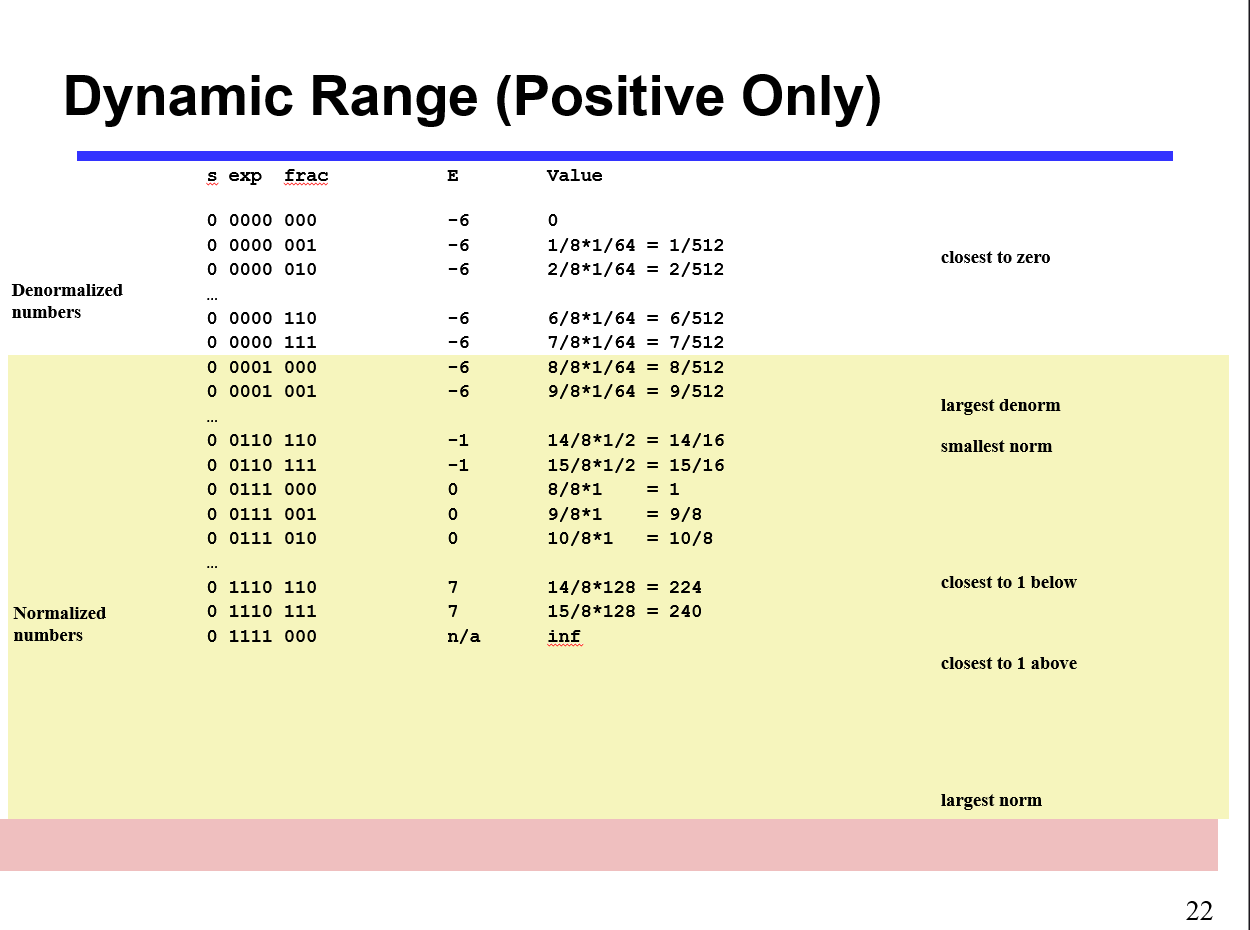
Denormalized Values & Encoding

In normalized value range, number lower than $1.0\times 2^{-126}$ is missing and undefined

In denormalized value range, numbers in than such range definates different meanings

Additionly, M in denormalized values will be regarded as $0.100…_2$ but not $1.100…_2$, and meanwhile the Exp is $000…0_2$ which means $\times2(^{-(n-2)})_1\kern{}_0$

normalized value cannot represent ZERO without denormalized version

1. $exp = 000…0; frac = 000…0$: Zero
2. $exp = 000…0; frac \ne 000…0$: Numbers close to zero
3. $exp = 111…1; frac = 000…0$: INF (infinity)
4. $exp = 111…1; frac \ne 000…0$: NaN (Not-a-Number)

1 & 2 show denormalized values whie 3 & 4 show another two special values

 

Special Properties

• FP Zero same as Integer Zero
• Can (Almost) Use Unsigned Integer Comparison
  • Must consider $0 = -0$
  • Must first compare sign bits
  • NaNs problematic

 

FP Operations

Rounding

Rounding Modes

• Towards zero
• Round down / floor()
• Round up / ceil()
• Nearest Even (default)

 

FP Addition

turn the smaller M to the bigger one, and shift the E

FP addition is NOT associative compared with Abelian Group

 

FP Mulitiplication

easy

M = M1 * M2
E = E1 + E2

FP mulitiplication is NOT associative or distributed over additions compared with Abelian Group

 

Non-Numeric Data

Logical Value

Alphanumeric Code

• ASCII : 7bit per char
• Unicode : 2Byte per char
• Chinese Character
  • Input Code
  • Internal Code
  • Font Code

 

Data Width & Storage