计算机系统I(三)

Basic Infomation

Teachers: wht, ll
Lab Docs: 浙江大学24年春夏系统贯通一实验( ZJU intranet required )

Because of some reasons, Chapter 04 should change position with Chapter 05

Chapter 04

Binary Logical & Gates

Three basic logical operations

• AND $\cdot$
• OR $+$
• NOT $^\prime\ \mathrm{or}\ \space\bar{}$

 

How to Model Logic Functions?

• Using Switches

 

Logic Gates

• Perform logic functions
  NOT, AND, OR, NAND, NOR, …
• Single-input
  NOT gate, buffer
• Two-input
  AND, OR, XOR, NAND, NOR, XNOR
• Multiple-input
  NOR3, AND4, …

NOT $Y=\overline{A}$

BUF $Y=A$

AND $Y=AB$ (straight on the input edge)

OR $Y=A+B$ (curly on the input edge)

XOR $Y=A\oplus B$ ( double curly edges )

NXOR $Y=\overline{ A\oplus B}$

NAND $Y=\overline{AB}$

NOR $Y=\overline{A+B}$

 

Transistors

Developing

Relays $\rightarrow$ Vacuum Cude $\rightarrow$ Transistor

• Tinier & Faster
• More Integration
• Less Consumption

Nvidia’s employees are all gone at p.m.

 

Integrated Circuit & Transistors

• Integrated Circuit IC
  • Transisitor-Transisitor Logic TTL
  • CMOS

Transistor Function

Implementation of Logic Gates with Transisitors

 

Chapter 06

TBD

 

Chapter 07

Boolean Algebra

Axioms

• $X\cdot Y$
• $X+Y$
• $\overline{X}$

Theorems: 1~3 Variables

See also here

Theorems: n Variables

De Morgans’s Theorem

$$\overline{F(X_1,X_2,…+X_n)}=F(\overline{X_1},\overline{X_2},…,\overline{X_n}),(+\ \mathrm{or}\ \cdot)$$

Shannon’s Theorem

$$F(X_1,X_2,…,X_n)=X_1\cdot F(1,X_2,…,X_n)+\overline{X_1}\cdot F(0,X_2,…,X_n)$$

$$F(X_1,X_2,…,X_n)=[X_1+F(0,X_2,…,X_n)]\cdot[\overline{X_1}+F(1,X_2,…,X_n)]$$

Power of Duality

If a formula is valid, its dual version is valid as well.

 

Logical Functions

Representation of Logic Functions

• Truth Table
• Waveform
• Boolean Expressions

Coplementation of Functions

• $+\iff\cdot$
• $0\iff1$
• Maintain the calculation order

Canonical & Standard Form

See also here

$f(x,y,z)=\sum(1,2,4,6)=\prod(0,3,5,7)$

$\sum(1,2,4,6)$ 代表最小项 minterms 列表
$\prod(0,3,5,7)$ 代表最大项 maxterms 列表

一个n变量逻辑函数的最小项列表编号集合约最大项列表编号集合的并集为n位编号全集{0, 1, …, 2n-1}，两者交集为空，是互补关系。
所以可以互相转换，只需对编码集合求补即可

作为一个例子, 我们可以把最小项理解为当二进制数 $\overline{xyz}$ 取 $m$ 时, $f(x,y,z)$ 取真;

同理, 最大项就是当二进制数 $\overline{xyz}$ 取 $M$ 时, $f(x,y,z)$ 取假;

 

Chapter 08

Simplification of Logic Functions

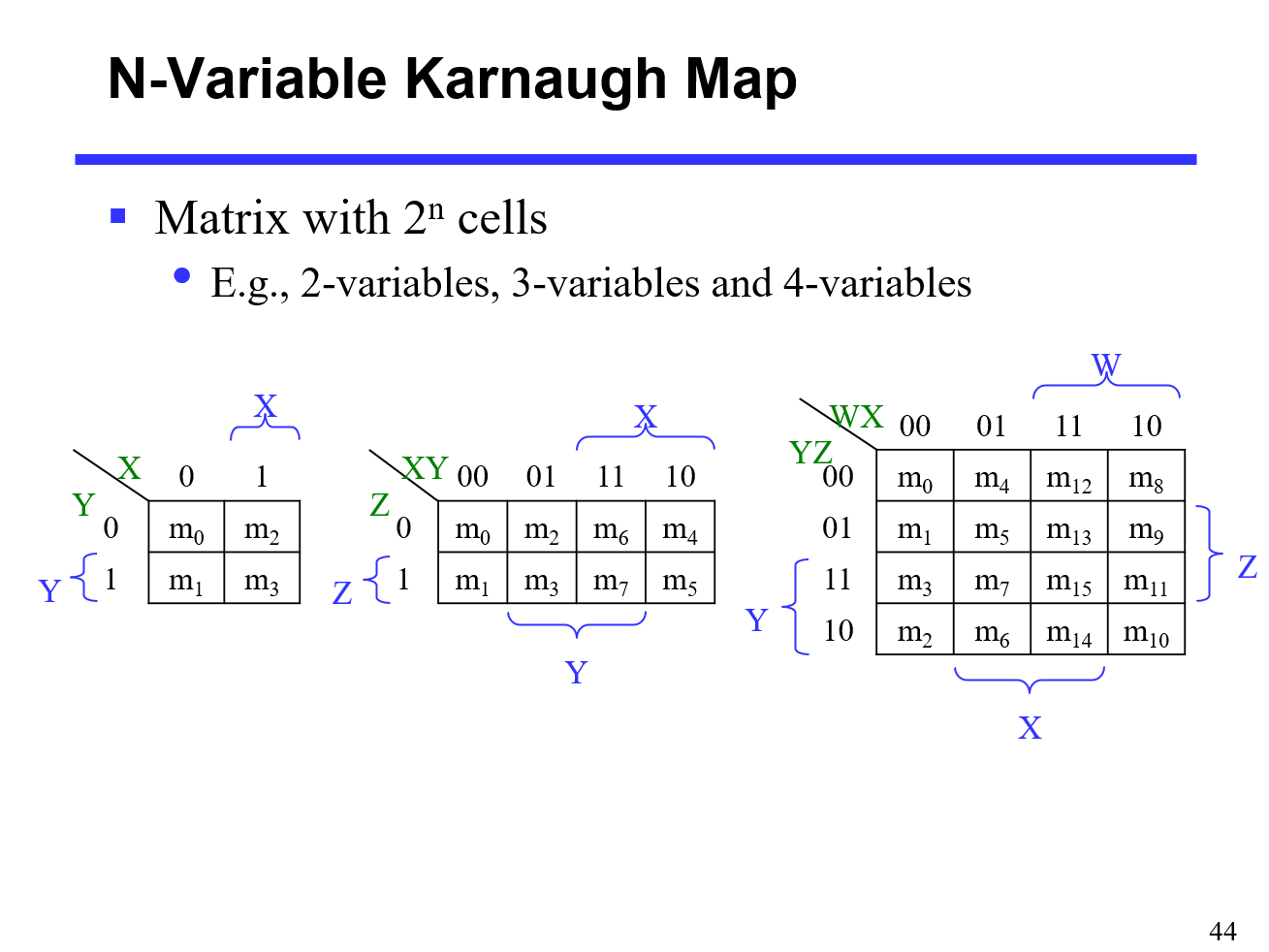
N-Variable Karnaugh Map

[Eg] 2-variables, 3-variables & 4 variables

每一行/列之间自由一个参数发生变化，01 不会和 10 相邻

化简卡诺图时，每个圈圈只会包括 $2^n$ 种情况，目的是最小化参数量

 

K-Map Definations

1. Implicant
2. Prime implicant
3. Essential prime implicant

no need to follow them strictly (scaping

 

Selection Rule Example with Don’t Cares

x could be regarded as both 0 & 1

x 是可 0 可 1的

 

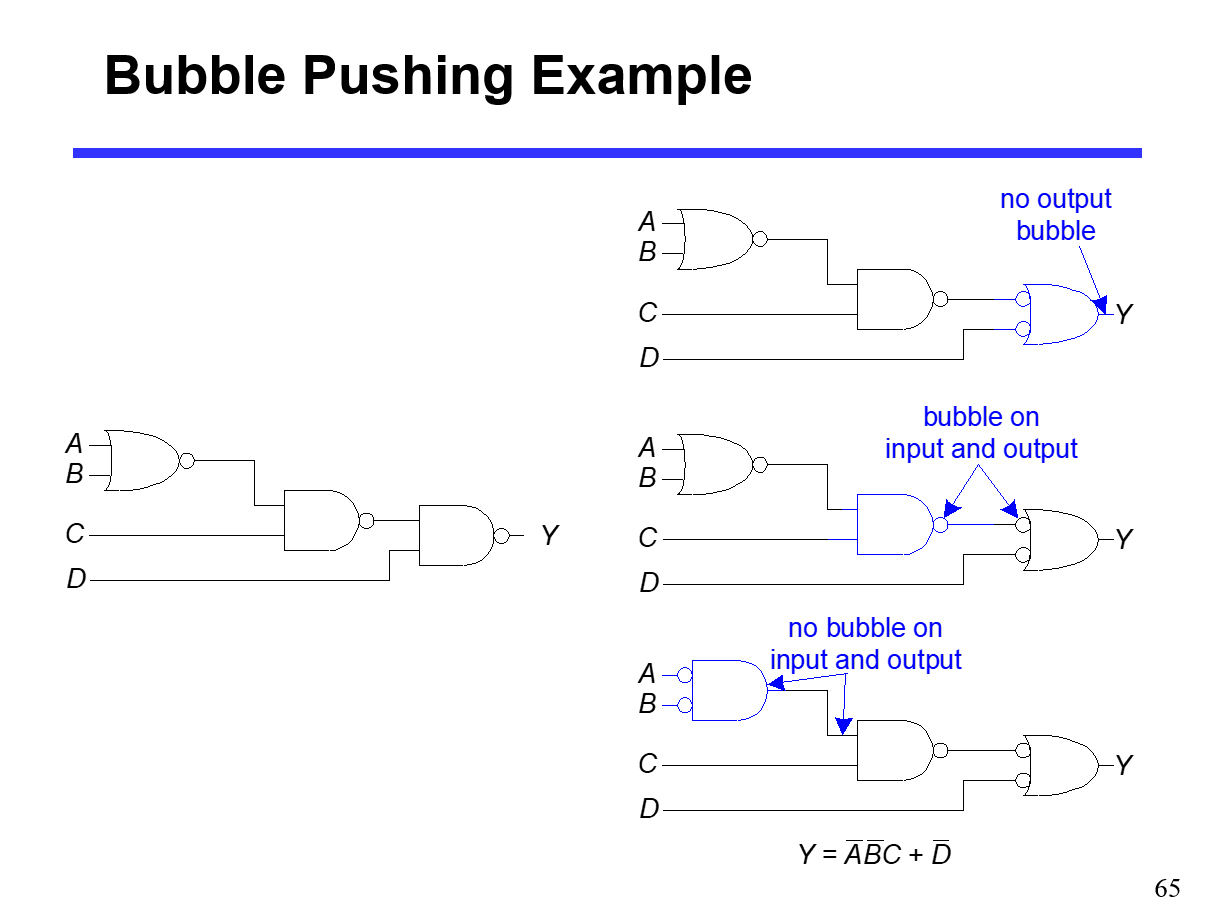
Bubble Pushing

a funny method to simplify the logical graph

pushing bubbles (NOT GATE) back & forward

Example